In honor of the latest meeting of our NEH sponsored Folger workshop, Early Modern Digital Agendas, I wanted to start a series of posts about how we find “distances” between texts in quantitative terms, and about what those distances might mean. Why would I argue that two texts are “closer” to one another than they are to a third that lies somewhere else? How do those distances shift when they are measured on different variables? When represented as points in different dataspaces, the distances between texts can shift as variables change — like a murmuration of starlings. So what kind of cloud is a cloud of texts?
In honor of the latest meeting of our NEH sponsored Folger workshop, Early Modern Digital Agendas, I wanted to start a series of posts about how we find “distances” between texts in quantitative terms, and about what those distances might mean. Why would I argue that two texts are “closer” to one another than they are to a third that lies somewhere else? How do those distances shift when they are measured on different variables? When represented as points in different dataspaces, the distances between texts can shift as variables change — like a murmuration of starlings. So what kind of cloud is a cloud of texts?
This first post begins with some work on the Folger Digital Texts of Shakespeare’s plays, which I’m making available in “stripped” form here. These texts were created by Mike Poston, who developed the encoding scheme for Folger Digital Texts, and who understands well the complexities involved in differentiating between the various encoded elements of a play text.
I’ve said the texts are “stripped.” What does that mean? It means that we have eliminated those words in the Folger Editions that are not spoken by characters. Speech prefixes, paratextual matter, and stage directions are absent from this corpus of Shakespeare plays. There are interesting and important reasons why these portions of the Editions are being set aside in the analyses that follow, and I may comment on that issue at a later date. (In some cases, stripping will even change the “distances” between texts!) For now, though, I want to run through a sequence of analyses using a corpus and tools that are available to as many people as possible. In this case that means text files, a web utility, and in subsequent posts on “dimension reduction,” an excel spreadsheet alongside some code written for the statistics program R.
The topic of this post, however, is “distance” — a term well worth thinking about as our work moves from corpus curation through the “tagging” of the text and on into analysis. As always, the goal of this work is to do the analysis and then return to these texts with a deepened sense of how they achieve their effects — rhetorically, linguistically, and by engaging aesthetic conventions. It will take more than one post to accomplish this full cycle.
So, we take the zipped corpus of stripped Folger Edition plays and upload it to the online text tagger, Ubiqu+ity. This tagger was created with support from the Mellon Foundation’s Visualizing English Print grant at the University of Wisconsin, in collaboration with the creators of the text tagging program Docuscope at Carnegie Mellon University. Uniqu+ity will pass a version of Docuscope over the plays, returning a spreadsheet with percentage scores on the different categories or Language Action Types (LATs) that Docuscope can tally. In this case, we upload the stripped texts and request that they be tagged with the earliest version of Docuscope available on the site, version 3.21 from 2012. (This is the version that Hope and I have used for most of our analyses in our published work. There may be some divergences in actual counts, as this is a new implementation of Docuscope for public use. But so far the results seem consistent with our past findings.) We have asked Ubiqu+ity to create a downloadable .csv file with the Docuscope counts, as well as a series of HTML files (see the checked box below) that will allow us to inspect the tagged items in textual form.
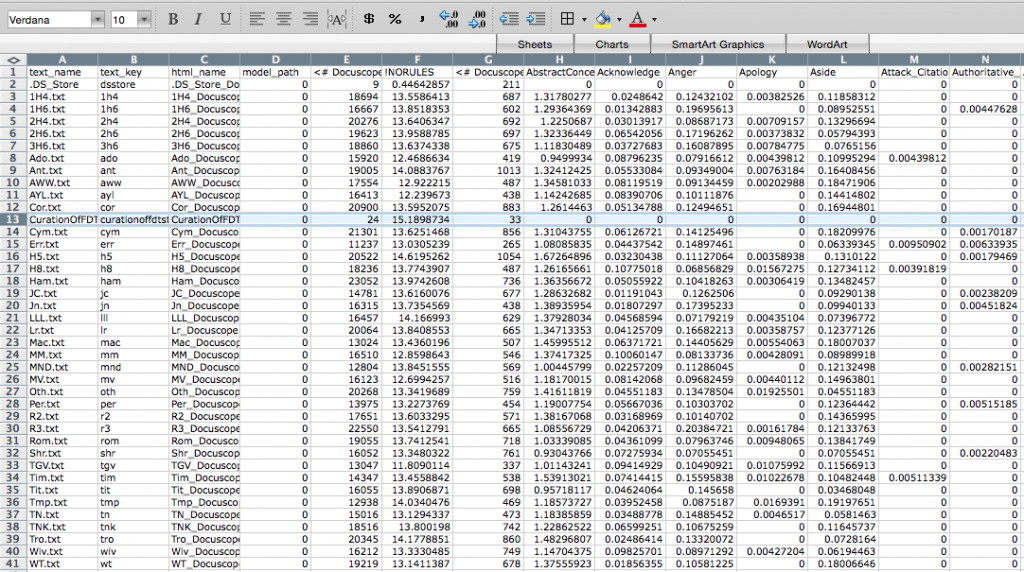
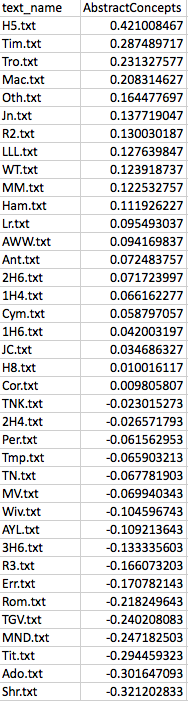
The results can be downloaded here, where you will find a zipped folder containing the .csv file with the Docuscope counts and the HTML files for all the stripped Folger plays. The .csv file will look like the one below, with abbreviated play names arrayed vertically in the first column, then (moving columnwise to the right) various other pieces of metadata (text_key, html_name, and model_path), and finally the Docuscope counts, labelled by LAT. You will also find that a note on curation was fed into the program. I will want to remove this row when doing the analysis.
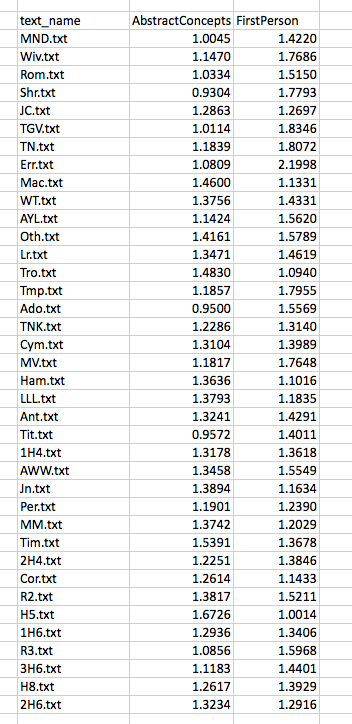
For ease of explication, I’m going to pare down these columns to three: the name of the text in column 1, and then the scores that sit further to the right on the spreadsheet for two LATs: AbstractConcepts and FirstPerson. These scores are expressed as a proportion, which to say, the number of all tokens tagged under this LAT as a fraction of all the included tokens. So now we are looking at something like this:
Before doing any analysis, I will make one further alteration, subtracting the mean value for each column (the “average” score for the LAT) from every score in that column. I do this in order to center the data around the zero point of both axes:
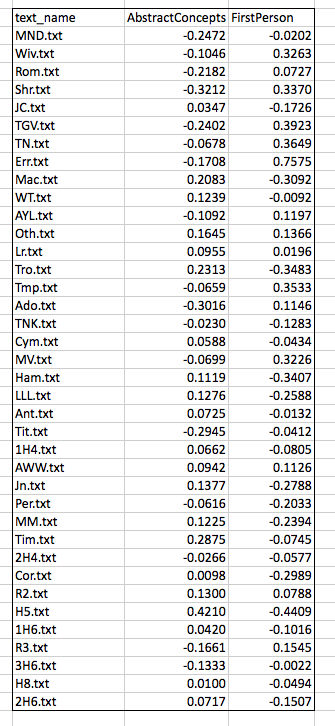 Now some analysis. Having identified a corpus (Shakespeare’s plays) and curated our texts (stripping, processing), we have counted some agreed upon features (Docuscope LATs). The features upon which we are basing the analysis are those words or strings of words that Docuscope counts as AbstractConcepts and FirstPerson tokens.
Now some analysis. Having identified a corpus (Shakespeare’s plays) and curated our texts (stripping, processing), we have counted some agreed upon features (Docuscope LATs). The features upon which we are basing the analysis are those words or strings of words that Docuscope counts as AbstractConcepts and FirstPerson tokens.
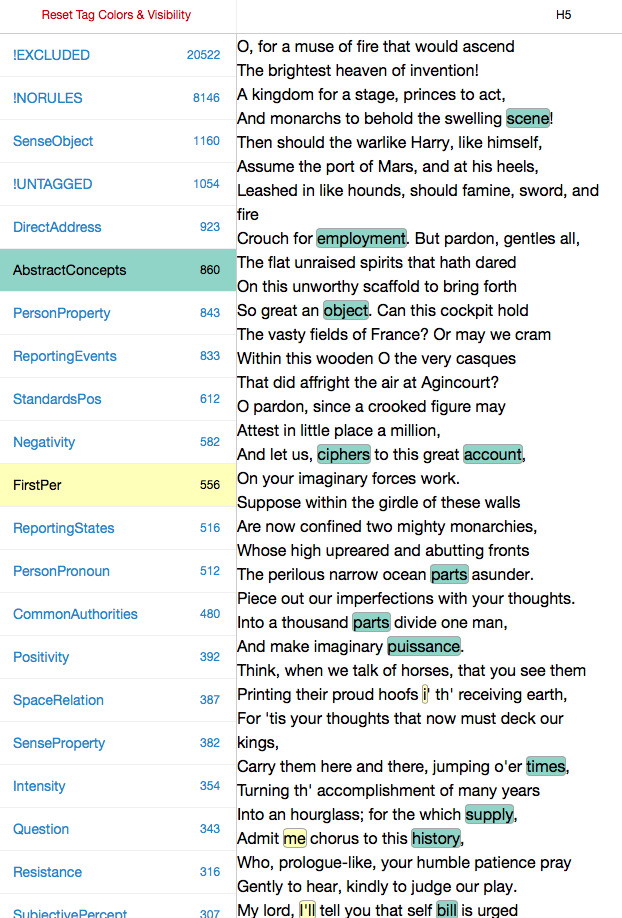
It’s important to note that at any point in this process, we could have made different choices, and that these choices would have lead to different results. The choice of what to count is a vitally important one, so we ought to give thought to what Douscope counted as FirstPerson and AbstractConcepts. To get to know these LATs better — to understand what exactly has been assigned these two tags —we can open one of the HTML files of the plays and “select” that category on the right hand side of the page, scrolling through the document to see what was tagged. Below is the opening scene of Henry V, so tagged:
Before doing the analysis, we will want explore the features we have been counting by opening up different play files and turning different LATs “on and off” on the left hand side of the HTML page. This is how we get to know what is being counted in the columns of the .csv file.
I look, then, at some of our texts and the features that Ubiqu+ity tagged within them. I will be more or less unsatisfied with some of these choices, of course. (Look at “i’ th’ receiving earth”!)Because words are tagged according to inflexible rules, I will disagree with some of the things that are being included in the different categories. That’s life. Perhaps there’s some consolation in the fact that the choices I disagree with are, in the case of Docuscope, (a) relatively infrequent and (b) implemented consistently across all of the texts (wrong in the same way across all types of document). If I really disagree, I have the option of creating my own text tagger. In practice, Hope and I have found that it is easier to continue to use Docuscope, since we do not want to build into the tagging scheme the self-evident things we may be interested in. It’s a good thing that Docuscope remains a little bit alien to us, and to everyone else who uses it.
Now to the question of distance.
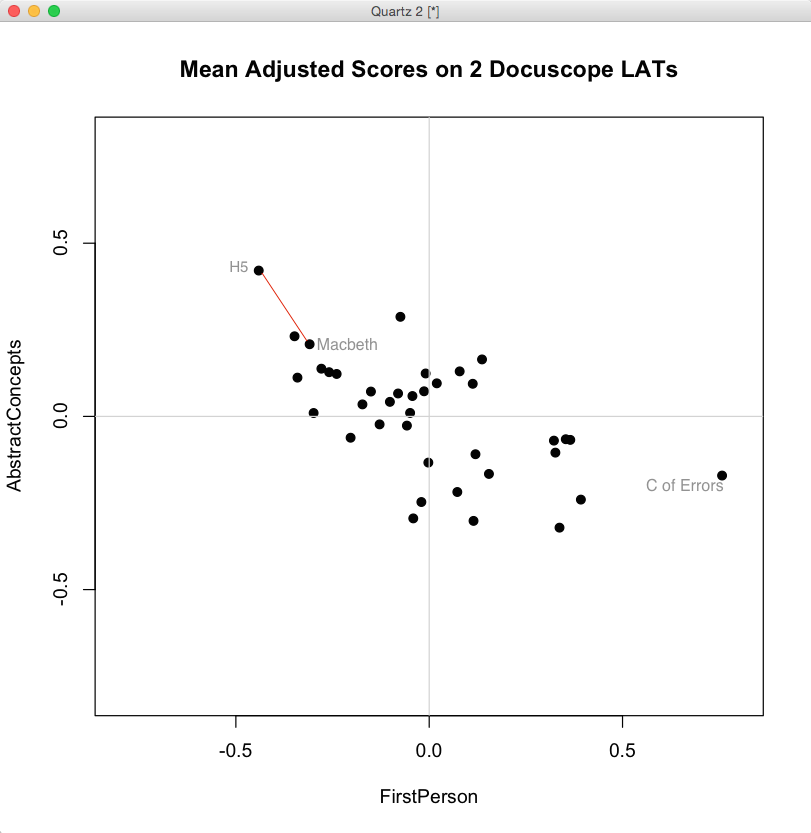
When we look at the biplot above, generated in R from the mean-adjusted data above, we notice a general shape to the data. We could use statistics to describe the trend — there is a negative covariance between FirstPerson and AbstractConcept LATs — but we can already see that as FirstPerson tokens increase, the proportion of AbstractConcept tokens tends to decrease. The trend is a rough one, but there is the suggestion of a diagonal line running from the upper left hand side of the graph toward the lower right.
What does “distance” mean in this space? It depends on a few things. First, it depends on how the data is centered. Here we have centered the data by subtracting the column means from each entry. Our choice of a scale on either axis will also affect apparent distances, as will our choice of the units represented on the axes. (One can tick off standard deviations around the mean, for example, rather than the original units, which we have not done). These contingencies point up an important fact: distance is only meaningful because the space is itself meaningful — because we can give a precise account of what it means to move an item up or down either of these two axes.
Just as important: distances in this space are a caricature of the linguistic complexity of these plays. We have strategically reduced that complexity in order to simplify a set of comparisons. Under these constraints, it is meaningful to say that Henry V is “closer” to Macbeth than it is to Comedy of Errors. In the image above, you can compare these distances between the labelled texts. The first two plays, connected by the red line, are “closer” given the definitions of what is being measured and how those measured differences are represented in a visual field.
When we plot the data in a two dimensional biplot, we can “see” closeness according to these two dimensions. But if you recall the initial .csv file returned by Ubiq+ity, you know that there can be many more columns — and so, many more dimensions — that can be used to plot distances.
What if we had scattered all 38 of our points (our plays) in a space that had more than the two dimensions shown in the biplot above? We could have done so in three dimensions — plotting three columns instead of two — but once we arrive at four dimensions we are beyond the capacity for simple visualization. Yet there may be a similar co-paterning (covariance) among LATs in these higher dimensional spaces, analogous to the ones we can “see” in two dimensions. What if , for example,the frequency of Anger decreases alongside that of AbstractConcepts just when FirstPerson instances increase? How should we understand the meaning of comparatives such as “closer together” and “further apart” in such multidimensional spaces? For that, we need techniques of dimension reduction.
In the next post, I will describe my own attempts to understand a common technique for dimension reduction known as Principal Component Analysis. It took about two years for me to figure that out, however imperfectly. I wanted to pass that along in case others are curious. But it is important to understand that these more complex techniques are just extensions of something we can imagine in more simpler terms. And it is important to remember that there are very simple ways of visualizing distance — for example, an ordered list. We assessed distance visually in the biplot above, a distance that was measured according to two variables or dimensions. But we could have just as easily used only one dimension, say, Abstract Concepts. Here is the list of Shakespeare’s plays, in descending order, with respect to scores on AbstractConcepts:
Even if we use only one dimension here, we can see once again that Henry V is “closer” to Macbeth than it is to Comedy of Errors. We could even remove the scores and simply use an ordinal sequence of this play, then this, then this. There would still be information about “distances” in this very simple, one dimensional, representation of the data.
Now we ask ourselves: which way of representing the distances between these tests is better? Well, it depends on what you are trying to understand, since distances — whether in one, two, or many more dimensions — are only distances according to the variables or features (LATs) that have been measured. In the next post, I’ll try to explain how the thinking above helped me understand what is happening in a more complicated form of dimension reduction called Principal Component Analysis. I’ll use the same mean adjusted data for FirstPerson and AbstractConcepts discussed here, providing the R code and spreadsheets so that others can follow along. The starting point for my understanding of PCA is an excellent tutorial by Jonathon Shlens, which will be the underlying basis for the discussion.